
 |
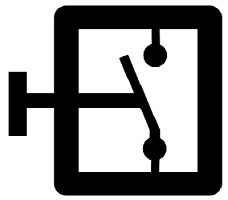
Der Tastsensor |
|
Mit Hilfe von Sensoren versuchen Robotersystem Umwelteinflüsse wahrzunehmen, sodass eine bestimmte gewünschte Reaktion vom Prozessor und den Aktoren ausgelöst werden kann. Tastsensoren bilden hierbei in ihrer Einfachheit die Grundlage der Sensorik. Sie werden durch physikalischen Druck ausgelöst und arbeiten nach dem Alles-oder-nichts-Prinzip: Wird ein bestimmter Schwellenwert überschritten, so wird ein vordefinierter Zustand entweder vollständig (alles) oder gar nicht (nichts) zurückgegeben, beispielsweise kann durch einen Tastsensor eine Lampe ein- beziehungsweise ausgeschaltet werden. In der digitalen Informationsverarbeitung muss dabei häufig eine bestimmte Spannung überschritten werden.
Grundsätzlich können Tastsensoren nach verschiedenen Merkmalen unterschieden werden, hier sei jedoch nur genauer auf die Art des Auslösens eingegangen: Bleibt der Tastsensor nach erfolgter Bestätigung stabil in seinem Zustand, so spricht man von Kippschaltern oder Rastschaltern. Taster hingegen kehren nach Wegnahme der Bestätigung in ihre Grundstellung oder Ausgangsstellung zurück.
Tastsensoren sind im Sinne der Informatik Schalter, die die Basis der digitalen Logik bilden, auf der sowohl Computer als auch Robotersysteme aufbauen. Insbesondere die Verknüpfung mehrerer Schalter hat zur Entwicklung der heutigen digitalen Systeme geführt.
Aber was sind nun die grundlegenden logischen Verknüpfungen von Schaltern?
Wie können diese Verknüpfungen technisch mit Schaltern oder Tastsensoren realisiert werden?
Übersicht:
| Bei elektrischen Schaltungen: | In der Halbleitertechnik: | Logischer Wert: | Weitere Bezeichnung: | |
| Tastsensor / Schalter ist gedrückt | Stromfluss | high | 1 | true |
| Tastsensor / Schalter ist nicht gedrückt | kein Stromfluss | low | 0 | false |
Digitaltechnik
Im Gegensatz zu analogen Schaltungen arbeiten digitale Schaltungen mit diskreten Signalen, die üblicherweise als logisch null (0) und logisch eins (1) bezeichnet werden. Eine besondere Bedeutung kommt dabei der logischen Verknüpfung zweier Schalter zu. Ein Fahrstuhl setzt sich beispielsweise nur in Bewegung falls einerseits die Lichtschranke an der Tür freigegeben wird und andererseits ein Stockwerk angewählt wurde. Hier müssen also beide Schalter „geschlossen“ sein um eine Bewegung in Gang zu setzen. Die zugehörige logische Operation bezeichnet man als AND.
Solche Operationen findet man auch bei Suchmaschinen im Internet: Werden etwa die Suchbegriffe „Wüste“ und „Afrika“ in den Suchfeldern eingegeben, so erhält man bei der logischen Verknüpfung der beiden Suchbegriffe mit AND nur Treffer zu Wüsten, die sich in Afrika befinden.
Andererseits können zwei Schalter aber auch mit der logischen Operation OR verknüpft werden. Ein Klingeln im Haus kann sowohl durch den Schalter am Gartentor als auch durch den Schalter direkt an der Haustür ausgelöst werden. Wendet man diese logische Operation auf Suchmaschinen an, so erhält man in obigem Beispiel alle Treffer zu Wüsten, alle Treffer zu Afrika und natürlich auch die Wüsten, die sich in Afrika befinden.
Binäre logische Operationen lassen sich durch sogenannte Wahrheitstabellen darstellen. Sie bilden die Grundlage der Booleschen Algebra und ist der Arbeit des britischen Mathematikers George Boole (1815-1864) zu verdanken. Sie unterscheidet drei Grundoperationen:
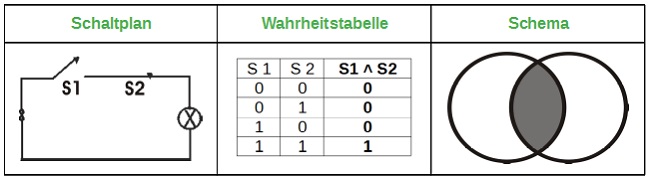
1. Die Konjunktion AND (S1 ˄ S2)
Zwei in Serie geschaltete Schalter bilden eine AND – Verknüpfung: Nur wenn beide Schalter geschlossen sind fließt Strom.
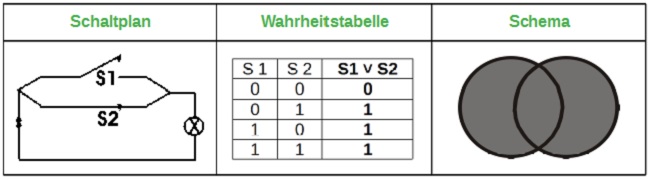
2. Die Disjunktion OR (S1 ˅ S2)
Zwei parallel geschaltete Schalter bilden eine OR - Verknüpfung: Wenn mindestens einer der beiden Schalter geschlossen ist, fließt Strom.
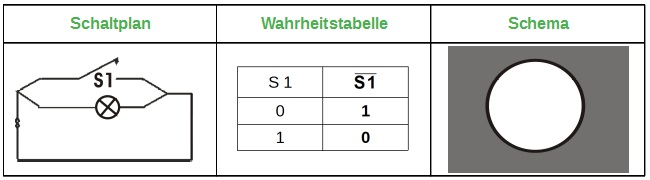
3. Die Negation NOT (S1)
Eine zu einem Schalter parallel geschaltete Lampe bildet eine NOT - Verknüpfung: Wenn der Schalter offen ist, fließt Strom.
Die logischen Operatoren AND, OR und NOT bilden die Grundoperationen, aus denen sich alle weiteren Operationen, wie zum Beispiel NAND, NOR oder XOR aufbauen lassen, so wie alle Farben aus drei Grundfarben rot, grün und blau gemischt werden können.

Aufgaben zur Verknüpfung von Schaltern
Aufgabe 1: AussagenWeitere Aufgaben zu logischen Verknüpfungen
Aufgabe 6: Vergleich